卫星伪距测量原理

定位导航
1647 字

一、伪距概念

伪距是GPS接收机对卫星信号的一个最基本的距离测量值，它并不是卫星与接收机之间的 真实几何距离，而是包含了各种误差的虚假距离因此得名。伪距的计算方式是光速与接收机和卫星之间时间差的乘积，因此一个精准的时间系统对于伪距测量来说是非常重要的。

1.1 时间系统

首先了解一下常用的时间系统：

类型 特点
世界时(UT)
  1. 基于地球自转的自然时间系统，即所说的”自然日”
  2. “平太阳”两次经过格林尼治子午线经过的时间为1天
  3. “平太阳”指沿赤道匀速运动，其速度等于真太阳全年平均速度的虚构太阳以解决
    太阳运动不均匀的问题
  4. 秒长定义为1/86400个平太阳日，由于地球自转变慢的缘故，UT扔按
    每年约1s的速度变慢
  5. 无固定起点，基于地球自转
国际原子时(TAI)
  1. 由全球数百台高精度原子钟加权平均产生
  2. 秒长严格定义为铯-133原子基态两个超精细能级间跃迁对应辐射的
    9,192,631,770个周期的持续时间
  3. 极其稳定、均匀，是纯物理的时间尺度与地球自转无关
  4. 1958 年 1 月 1 日 00:00:00 UTC起
协调世界时(UTC)
  1. UTC是TAI和UT之间的折中方案
  2. 严格的以精确的国际原子时秒长为基础，当协调时与世界时差距
    超过0.9s时，采用润秒的方式加1s尽量接近世界时
  3. 1960 年左右开始使用，正式标准化于 1972 年 1 月 1 日 00:00:00 UTC
GPS时间(GPST)
  1. 基于原子钟
  2. 与 TAI 和 UTC 的秒长一致
  3. 与 TAI 固定少19秒，与 UTC 差值视润秒而定
  4. 1980 年 1 月 6 日 00:00:00 UTC起

为了更好的理解 GPS 时间与其他时间系统的关系，这里引用一段话来做解释：

GPS时间的原点是这样规定的: GPS时间的零时刻与协调时(UTC)的1980年1月6日零时刻一致，此刻起 GPS 时间开始周而复始的计算，同时也正好在这一刻，GPS 时间和协调时（UTC）均落后国际原子钟（TAI）19秒。

1. “GPS时间的零时刻与协调时的1980年1月6日零时刻一致”

  • GPS时间（GPST） 是一个由GPS系统内部产生和维持的连续原子时尺度，它不使用闰秒。
  • 它的起点（历元）被定义为 UTC时间 1980年1月6日 00:00:00。
  • 这意味着，在1980年1月6日 00:00:00 UTC 这一瞬间，GPS时间的计数器被设置为 0周，0秒。

2. “此刻起GPS时间开始周而复始的计算”

  • 从那个起点开始，GPS时间就像一辆永不停歇、匀速前进的列车，只使用原子秒的长度来累积时间。
  • 它采用“周数”和“周内秒”的计数方式（一周 = 604,800秒），从起点开始累加没有间断。这是“周而复始”的含义。

3. “同时也正好在这一刻，GPS时间和协调时均落后国际原子钟19秒”

  • 这是最核心的一点，它揭示了TAI、UTC和GPST在起点时刻的关系。
  • 国际原子时（TAI）从1958年起点开始，一秒都未曾停顿地走到了1980年。
  • 世界时（UT）从1958年1月到1972年1月之间已经比国际原子时（TAI）慢了约10秒
  • 协调世界时（UTC）在1972年1月确立机制时考虑了这个偏差，规定初始时刻的 TAI 与 UTC 的差值为 10秒（即 TAI - UTC = 10 s）
  • 1972-1980年间 UTC 增加了9秒闰秒，因此，在1980年1月6日这个GPS时间的起点上，存在固定的差值19秒

1.2 计算原理

如下图所示，涉及三种时间系统：各颗GPS卫星时间、各台接收机时钟以及统一前两者时间标准的GPS时系。

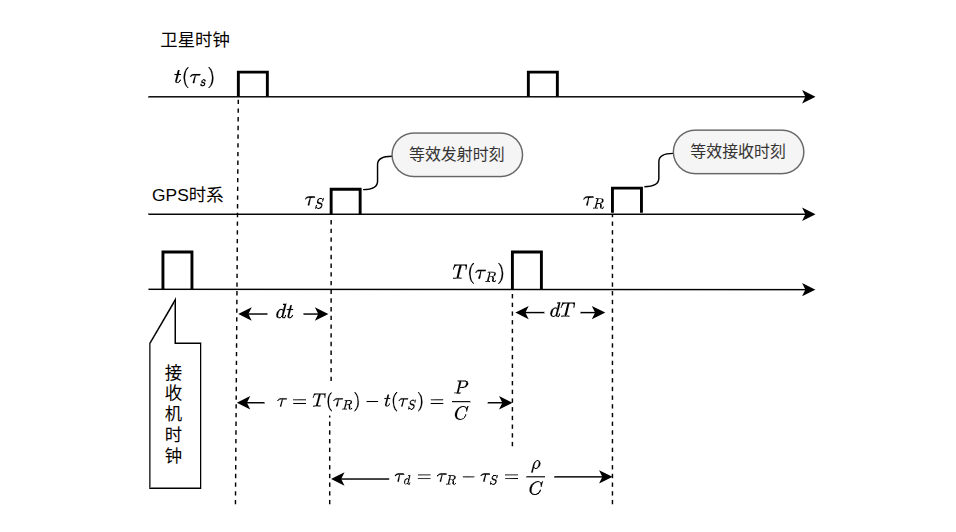
图中：

  • $t(\tau_{S})$——GPS卫星发射时刻
  • $T(\tau_{R})$——GPS卫星信号到达接收机的时刻
  • $\tau_{S}$——对应的在GPS时系下的信号发射时刻
  • $\tau_{R}$——对应的在GPS时系下的信号接收时刻
  • $\tau_{d}$——卫星信号的真实传播时间
  • $P$——伪距
  • $\rho$——卫星和接收机之间的真实距离
  • $C$——光速
  • $\tau$——从GPS卫星到接收机的传播时间

这样则可得：

$$\tau = T(\tau_{R}) - t(\tau_{S})$$

进一步转换：

$$\tau = T(\tau_{R}) - t(\tau_{S}) + (\tau_{R} - \tau_{S}) - (\tau_{R} - \tau_{S}) = \\ (\tau_{R} - \tau_{S}) + [\tau_{S} - t(\tau_{S})] - [\tau_{R} - T(\tau_{R})] = \\ (\tau_{R} - \tau_{S}) + (dt - dT)$$

式中：

$dt$——卫星时钟相对于GPS时系的时间偏差，可根据卫星导航电文中给出的参数求得，故可以视为已知量。
$dT$——接收机时钟相对于GPS时系的时间偏差。

这样可得伪距计算公式如下：

$$P = C \cdot \tau = C \cdot (\tau_{R} - \tau_{S}) + C \cdot (dt- dT)$$

又卫星与接收机之间的真实距离可表示为：
$$\rho = C \cdot (\tau_{R} - \tau_{S}) = C\tau_{d}$$

则伪距可表示为：

$$P = C \cdot \tau =\rho + C \cdot (dt- dT) + d_{ion} + d_{trop} + \varepsilon_{\rho}$$

式中：$C(dt-dT)$——时钟偏差引起的距离偏差
$d_{ion}$——电离层效应引起的距离偏差，可通过模型估计，认为已知
$d_{trop}$——对流层引起的距离偏差，可通过模型估计，认为已知
$\varepsilon_{\rho}$——代表所有未直接体现在式中的误差总和，此处可以暂且忽略

伪距方程中 $\rho$ 是卫星位置和用户接收机位置的函数，所以第 $i$ 颗卫星测得的伪距可以写作：

$$P^{i} = \sqrt{ [X^{i}(t) - X_{u}(t)]^{2}+[Y^{i}(t) - Y_{u}(t)]^{2}+[Z^{i}(t) - Z_{u}(t)]^{2}}+C(dt^{i}-dT)+d_{ion}^{i}+d_{trop}^{i} + \varepsilon_{\rho}^{i} $$

其中 $X^{i}(t),Y^{i}(t),Z^{i}(t)$ 表示第 i 颗卫星在 t 时刻的三维坐标，这可从星历数据中计算，即为已知数；$X^{u}(t),Y^{u}(t),Z^{u}(t)$ 表示的是用户接收机在 t 时刻的三维坐标，这是待求解的未知数；加上接收机钟差 $dT$ ，一共有四个未知数，因此至少需要4颗卫星才可计算伪距。

//