一、几何解释
牛顿、拉弗森曾各自提出解决高次方程的方法,最后被合称为牛顿-拉弗森方法或称牛顿迭代法。这种方法的思路就是:切线是曲线的线性逼近,怎么理解呢?假如存在一个函数$f(x)=x^{2}$,我们随便选取$f(x)$上的点$(a,f(a))$做它的切线:
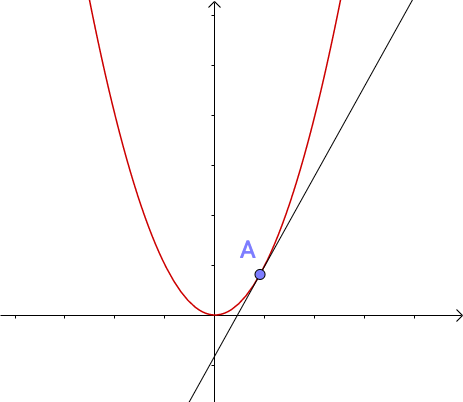
当在 A 点放大时,可以看出切线和函数$f(x)$非常接近。很显然,如果进一步放大图像,A 点切线就越接近$f(x)$。因为切线是一条直线(也就是线性的),那就可以说 A 点的切线是f(x)的线性逼近。离A点距离越近,这种逼近的效果也就越好,也就是说,切线与曲线之间的误差越小。所以我们可以说在A点附近,”切线 $\approx f(x)$”。
相对复杂函数的根,显然切线的根研究起来非常容易,既然切线可以近似于曲线,那么能否通过切线来研究复杂函数的根呢?存在这样一个事实:
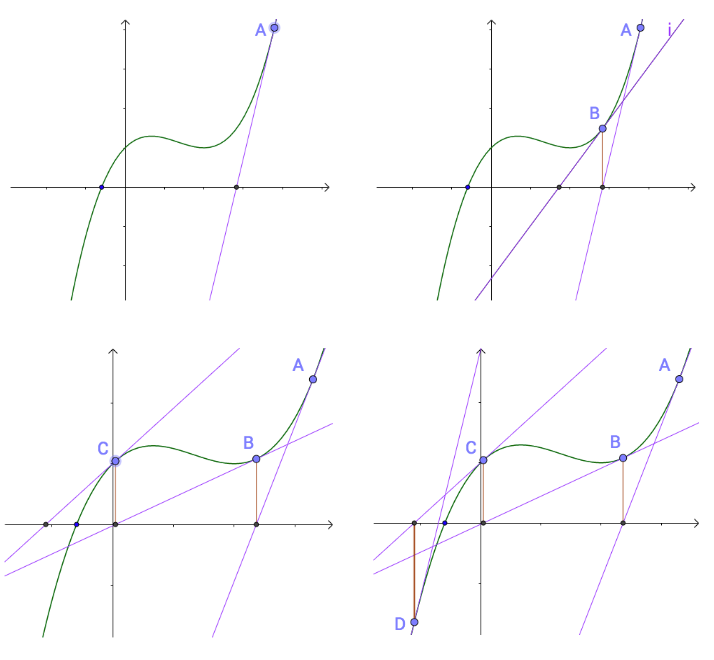
随便找一个曲线上的 A 点(为什么随便找,根据切线是切点附近的曲线的近似,应该在根点附近找,但是很显然我们现在还不知道根点在哪里),做一个切线,切线的根(就是和x轴的交点)与曲线的根,还有一定的距离。从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作;显然当过 D 切点的切线的根和函数的解已经非常接近!我们有理由相信当经过足够多次迭代之后我们得到的切线的根会无线接近曲线的根,这从数学术语来说是:迭代收敛了;
已知曲线方程$f(x)$,选取$x_{n}$点做切线,求$x_{n+1}$:
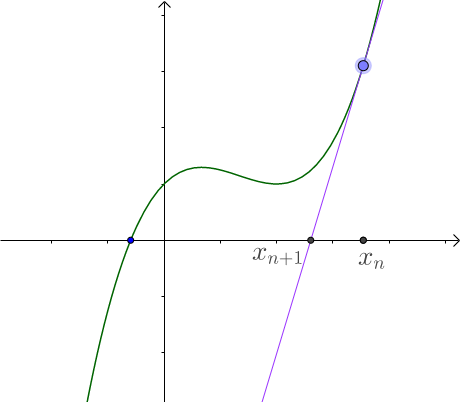
显然根据斜率公式可得:
$$\frac{f(x_{n+1}) - f(x_{n})}{x_{n+1}-x_{n}} = f’(x_{n}) \Rightarrow \\ x_{n+1} = x_{n} - \frac{f(x_{n})}{f’{(x_{n})}}$$
二、代数求解
虽然几何方法更直观,但现在很多教材使用泰勒展开式来推导牛顿法:
在$x_{n}$附近,将$f(x)$展开到一阶:
$$f(x_{n+1}) \approx f(x_{n}) + f’(x_{n})(x_{n+1}-x_{n})$$
我们想找到$f(x)=0$的解,于是近似式为零:
$$0 = f(x_{n+1}) + f’(x_{n})(x_{n+1}-x_{n})$$
解得:
$$x_{n+1} = x_{n} - \frac{f(x_{n})}{f’{x_{n}}}$$
这就是我们说的牛顿迭代公式
几何方式与泰勒展开方式的关系可如下表所示:
| 特征 | 几何(切线)视角 | 泰勒展开视角 |
|---|---|---|
| 本质 | 几何直观的方法是公式的解释 |
数学分析方法是公式的来源 |
| 优点 | 极其直观,容易理解和记忆, 提供了清晰的图像化思考 |
严谨,具有普适性,且便于分析收敛性, 可以推广到更复杂的情况(如多元函数) |
| 关系 | 外在表现与等价解释 | 内核与基础 |
三、解算速度
从几何上看,线性化是“沿着切线走”,直觉上知道它会很快逼近解,但“为什么这么快”是本节需要讨论的:
- 局部简化:泰勒一阶展开把非线性函数变成线性模型,便于分析和计算
- 明确方向:线性化后能快速得到改进方向(如梯度)
- 可迭代:每一步都重新线性化,逐步逼近真实解,稳定且高效
- 快速收敛:这正是通过泰勒展开提供的严谨数学解释
泰勒展开揭示“误差如何缩小”——这才是“快”的本质。在牛顿法迭代公式中,我们想知道:误差$e_{n} = x_{n} - r$ (r为真实根)是如何迭代减小的?
对$f(x_{n})$在真实根$r$附近做二阶泰勒展开:
$$f(x_{n}) = f(r) + f’(r)(x_{n}-r)+\frac{f’’(\xi)}{2}(x_{n}-r)^2 \ \ \ \ (其中\xi在r和x_{n})之间$$
由于$f(r)=0$,所以:
$$f(x_{n}) = f’(r)e_{n} + \frac{f’’(\xi)}{2}e_{n}^2$$
代入牛顿迭代公式则有:
$$x_{n+1} = x_{n} - \frac{f(x_{n})}{f’{(x_{n})}} \Rightarrow e_{n+1} = e_{n} - \frac{f(x_{n})}{f”{x_{n}}}$$
将上面的$f(x_{n})$和$f’(x_{n}) \approx f’(r) + f’’(r)(x_{n}-r)$代入,可以推导出:
$$e_{n+1} \approx \frac{f’’(r)}{2f’(r)}e_{n}^2$$
进一步表示为:
$$|e_{n+1}| \le C|e_{n}|^2$$
这样可以得出误差是平方级缩小!这叫做二阶收敛。
四、存在的问题
牛顿迭代法对于初始值非常敏感,如果初始值选的不好,可能出现:
- 不收敛
- 收敛到错误的根(非目标根)
- 在局部振荡或者发散
- 导数约等于0导致的数据爆炸
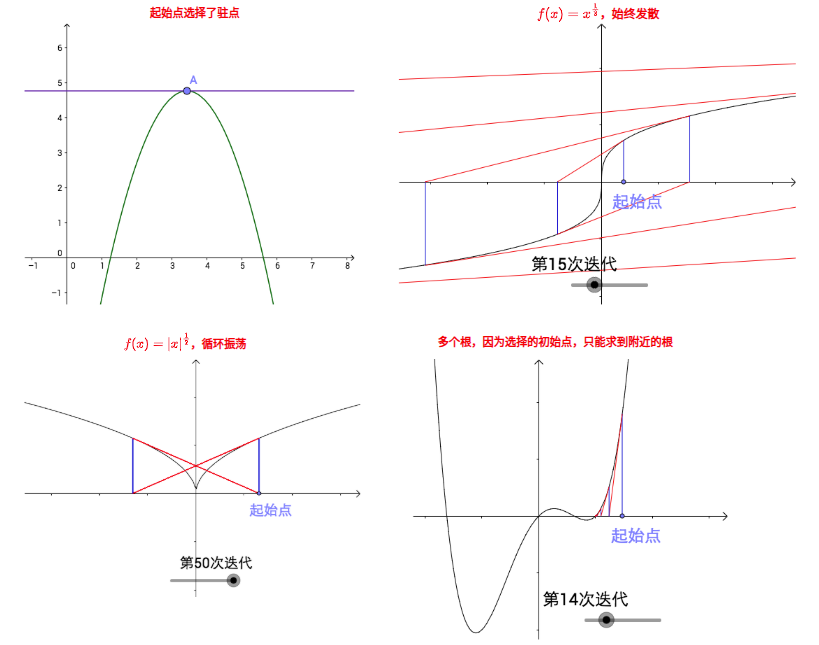
这就需要我们在面对的实际问题中引入其他的解决方式去尽可能的消除这种缺陷的影响。
五、牛顿迭代法的工程应用
5.1 基本概念
在卫星伪距测量原理一文中,我们推导出了GPS伪距观测方程:
$$P^{i} = \sqrt{ [X^{i}(t) - X_{u}(t)]^{2}+[Y^{i}(t) - Y_{u}(t)]^{2}+[Z^{i}(t) - Z_{u}(t)]^{2}}+C(dt^{i}-dT)+d_{ion}^{i}+d_{trop}^{i} + \varepsilon_{\rho}^{i} $$
去掉可以通过模型计算的对流层、电离层误差,系统其余的误差总和(太小),将钟差部分简化为$b$之后,可得伪距观测方程如下:
$$P_{i} = \sqrt{(x - x_{i})^{2}+(y - y_{i})^{2}+(z - z_{i})^{2}}+b$$
其中:
- $P_{i}$:第i颗卫星的伪距测量值(单位:米)
- $(x_{i},y_{i},z_{i})$:第i颗卫星在地心地固坐标系(ECEF)中的位置(已知,来自星历)
- $(x,y,z)$:接收机在ECEF中的未知位置
- $b$:光速与钟差的乘积(单位:米),未知量
我们定义真实几何距离:
$$r_{i} = \sqrt{(x - x_{i})^{2}+(y - y_{i})^{2}+(z - z_{i})^{2}}$$
所以观测方程可以描述为:
$$P_{i} = r_{i} + b$$
对于每一颗卫星,定义残差(误差)方程:
$$f_{i}(x,y,z,b) = r_{i}+b-P_{i}$$
我们希望残差为0,即$f_{i} = 0$,也就是说:找到一个位置和时钟偏差,使得预测值等于测量值。当有4颗卫星时,就得到4个残差方程,令
$$X = [x,y,z,b]^{T}$$
则整理为向量函数形式可得:
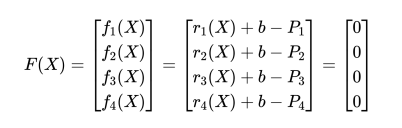
其中:
| 符号 | 含义 |
|---|---|
| $X \in \mathbb{R} ^{4}$ | 状态向量(待求解):位置+时钟偏差 |
| $F(X) \in \mathbb{R} ^{4}$ | 残差向量:每颗卫星的伪距误差 |
| $F(X)=0$ | 我们的目标:所有伪距误差为0 |
向量函数:将多个相关的函数”打包”成一个向量输出,方便我们用矩阵和向量的方法统一处理;在本例中我们的目标是让向量函数输出零向量;用牛顿法迭代时,雅可比矩阵就是这个向量函数的”导数矩阵”
5.2 计算步骤
步骤1:设定初始值
选择一个合理的初始猜测,例如:
- 地球质心附近:$x_{0} = 0,y_{0}=0,z_{0}=0$
- 或者地球表面某点(如WGS84椭球上的点)
- 时钟偏差初值:$b^{0}=0$(假设无偏差)
设:
$$X^{0} = [x_{0},y_{0},z_{0},b_{0}]^{T}$$
步骤2:计算每一颗卫星的残差
对于每一步k计算:
1、残差向量:$F(X^{(k)})$
① 计算当前估计位置到卫星的向量
$$\bigtriangleup x_{i} = x^{(k)} - x_{i} \ \, \ \ \bigtriangleup y_{i} = y^{(k)} - y_{i} \ \, \ \ \bigtriangleup z_{i} = z^{(k)} - z_{i}$$
② 计算几何距离
$$r_{i}^{k} = \sqrt{(\bigtriangleup x_{i})^{2}+(\bigtriangleup y_{i})^{2}+(\bigtriangleup z_{i})^{2}}$$
③ 计算残差
$$f_{i} = r_{i}^{(k)} + b^{(k)} - P_{i}$$
则可得残差向量$F = [f_{1},f_{2},f_{3},f_{4}]^{T}$
2、构建雅可比矩阵$J(X^{(k)}) = \frac{\partial F}{\partial X}|_{X^{(K)}} $
雅可比矩阵其实就是多元函数导数在高维空间的推广;对于多元函数,输入和输出都可能是向量,所以“变化率”不再是一个简单的数字,而需要一个矩阵来描述每个输入分量对每个输出分量的影响程度。这个矩阵就是雅可比矩阵。
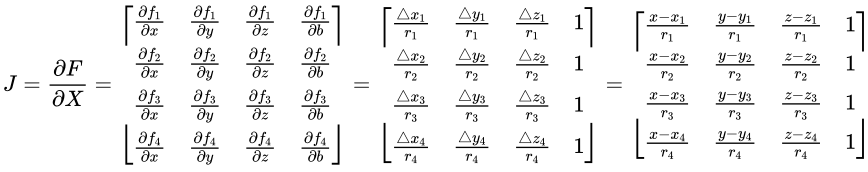
从矩阵中可以得出:
- 第
i行表示第i颗卫星的观测对状态变量的敏感度 - 第
i行表示从接收机指向卫星的单位方向向量 - 从左到右,前3列分表表示所有卫星的视线方向在X/Y/Z轴的投影(单位向量分量)
- 时钟偏差对所有伪距的影响相同
步骤3:解线性方程,求修正量$\bigtriangleup X$
线性展开得:
$$F(X+\bigtriangleup X) \approx F(X) + J\bigtriangleup X$$
令$F(X+\bigtriangleup X)=0$得:
$$\bigtriangleup X = -J^{-1}F$$
算得 $\bigtriangleup X = [\bigtriangleup x_{\xi},\bigtriangleup y_{\xi},\bigtriangleup z_{\xi},\bigtriangleup b_{\xi}]^{T}$
注意:实际编程中应使用数值稳定的方法求解(如 LU 分解、SVD),而不是直接求逆。
步骤4:更新状态向量
$$X^{(k+1)} = X^{k} + \bigtriangleup X $$
即:
$$x^{(k+1)} = x^{(k)} + \bigtriangleup x_{\xi} \\ y^{(k+1)} = y^{(k)} + \bigtriangleup y_{\xi} \\ z^{(k+1)} = z^{(k)} + \bigtriangleup z_{\xi} \\ b^{(k+1)} = b^{(k)} + \bigtriangleup b_{\xi}$$
步骤5:检查收敛
判断修正值$\bigtriangleup X$的模是否足够小,因为当修正值足够小时,解趋于稳定,说明已经接近真实解,例如:
- $\sqrt{(\bigtriangleup x_{\xi})^{2}+(\bigtriangleup y_{\xi})^{2}+(\bigtriangleup z_{\xi})^{2}} < 10^{-6}$米
- $\bigtriangleup b_{\xi} < 10^{-6}$米
满足条件则认为收敛,停止迭代;否则返回步骤2;
